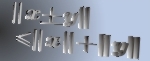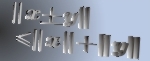| |
|
|
| |
Volume 10, Issue 3, Article 68 |
|
|
|
|
|
| |
An Unconstrained Optimization Technique for Nonsmooth Nonlinear Complementarity Problems
|
| |
|
Authors: |
M. Tawhid, |
|
| |
|
Keywords:
|
Nonlinear complementarity problem, unconstrained minimization, NCP function, merit function, regularity conditions, nonsmooth function, descent algorithm. |
|
| |
|
Date Received:
|
13/07/2009 |
|
| |
|
Date Accepted:
|
22/07/2009 |
|
| |
|
Subject Codes: |
90C33, 90C20, 90C56, 49J52
|
|
| |
|
Editors: |
Ram U. Verma, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this article, we consider an unconstrained minimization formulation of the nonlinear complementarity problem NCP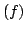 when the underlying functions are when the underlying functions are 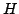 -differentiable but not necessarily locally Lipschitzian or directionally differentiable. We show how, under appropriate regularity conditions on an -differentiable but not necessarily locally Lipschitzian or directionally differentiable. We show how, under appropriate regularity conditions on an 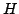 -differential of -differential of 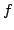 , minimizing the merit function corresponding to , minimizing the merit function corresponding to 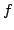 leads to a solution of the nonlinear complementarity problem. Our results give a unified treatment of such results for leads to a solution of the nonlinear complementarity problem. Our results give a unified treatment of such results for 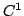 -functions, semismooth-functions, and for locally Lipschitzian functions. We also show a result on the global convergence of a derivative-free descent algorithm for solving nonsmooth nonlinear complementarity problem. -functions, semismooth-functions, and for locally Lipschitzian functions. We also show a result on the global convergence of a derivative-free descent algorithm for solving nonsmooth nonlinear complementarity problem.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|