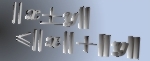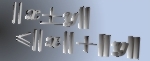| |
|
|
| |
Volume 4, Issue 5, Article 98 |
|
|
|
|
|
| |
Asymptotic Behaviour of Some Equations in Orlicz Spaces
|
| |
|
Authors: |
D. Meskine, A. Elmahi, |
|
| |
|
Keywords:
|
Strongly nonlinear elliptic equations, Natural growth, Truncations, Variational inequalities, Bilateral problems. |
|
| |
|
Date Received:
|
26/03/03 |
|
| |
|
Date Accepted:
|
05/08/03 |
|
| |
|
Subject Codes: |
35J25,35J60.
|
|
| |
|
Editors: |
Alberto Fiorenza, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we prove an existence and uniqueness result for solutions of some bilateral problems of the form where 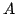 is a standard Leray-Lions operator defined on is a standard Leray-Lions operator defined on 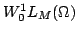 , with , with 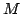 an N-function which satisfies the an N-function which satisfies the 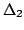 -condition, and where -condition, and where 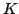 is a convex subset of is a convex subset of 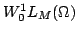 with obstacles depending on some Carathéodory function with obstacles depending on some Carathéodory function 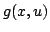 . We consider first, the case . We consider first, the case 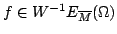 and secondly where and secondly where 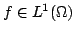 . Our method deals with the study of the limit of the sequence of solutions . Our method deals with the study of the limit of the sequence of solutions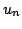 of some approximate problem with nonlinearity term of the form of some approximate problem with nonlinearity term of the form 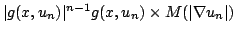 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|