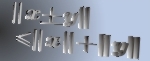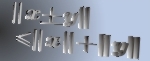|
We study the boundary of the region of weighted analytic centers for linear matrix inequality constraints. Let  be the convex subset of be the convex subset of 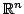 defined by defined by 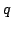 simultaneous linear matrix inequalities (LMIs) simultaneous linear matrix inequalities (LMIs) where 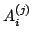 are symmetric matrices and are symmetric matrices and  . Given a strictly positive vector . Given a strictly positive vector      , the weighted analytic center , the weighted analytic center 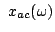 is the minimizer of the strictly convex function is the minimizer of the strictly convex function over  . The region of weighted analytic centers, . The region of weighted analytic centers,  , is a subset of , is a subset of  . We give several examples for which . We give several examples for which  has interesting topological properties. We show that every point on a central path in semidefinite programming is a weighted analytic center. has interesting topological properties. We show that every point on a central path in semidefinite programming is a weighted analytic center. We introduce the concept of the frame of  , which contains the boundary points of , which contains the boundary points of  which are not boundary points of which are not boundary points of  . The frame has the same dimension as the boundary of . The frame has the same dimension as the boundary of  and is therefore easier to compute than and is therefore easier to compute than  itself. Furthermore, we develop a Newton-based algorithm that uses a Monte Carlo technique to compute the frame points of itself. Furthermore, we develop a Newton-based algorithm that uses a Monte Carlo technique to compute the frame points of  as well as the boundary points of as well as the boundary points of  that are also boundary points of that are also boundary points of  . .
|