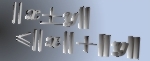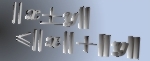| |
|
|
| |
Volume 6, Issue 2, Article 32 |
|
|
|
|
|
| |
On Hyers-Ulam Stability of a Special Case of O'Connor's and Gajda's Functional Equations
|
| |
|
Authors: |
Belaid Bouikhalene, Elhoucien Elqorachi, Ahmed Redouani, |
|
| |
|
Keywords:
|
Functional equations, Hyers-Ulam stability, Gelfand pairs. |
|
| |
|
Date Received:
|
08/11/04 |
|
| |
|
Date Accepted:
|
01/03/05 |
|
| |
|
Subject Codes: |
39B72.
|
|
| |
|
Editors: |
Kazimierz Nikodem, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we obtain the Hyers-Ulam stability for the following functional equation where 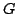 is a locally compact group, is a locally compact group, 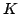 is a compact subgroup of is a compact subgroup of 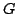 , , 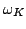 is the normalized Haar measure of is the normalized Haar measure of 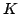 , , 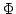 is a finite group of is a finite group of 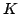 -invariant morphisms of -invariant morphisms of 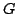 and and 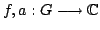 are continuous complex-valued functions such that are continuous complex-valued functions such that 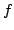 satisfies the Kannappan type condition satisfies the Kannappan type condition 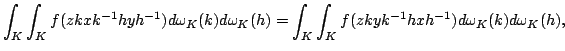 | (*) |
for all 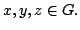
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|