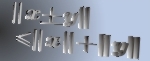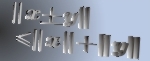| |
|
|
| |
Volume 7, Issue 3, Article 101 |
|
|
|
|
|
| |
The Dual Spaces of the Sets of Difference Sequences of Order $m$
|
| |
|
Authors: |
C.A. Bektas, Mikhail Et, |
|
| |
|
Keywords:
|
Difference sequences, $alpha -$, $beta -$ and $gamma -$duals. |
|
| |
|
Date Received:
|
16/12/05 |
|
| |
|
Date Accepted:
|
07/01/06 |
|
| |
|
Subject Codes: |
40C05, 46A45.
|
|
| |
|
Editors: |
Alexander G. Babenko, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The idea of difference sequence spaces was introduced by Kizmaz [5] and the concept was generalized by Et and Çolak [3]. Let 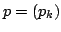 be a bounded sequence of positive real numbers and be a bounded sequence of positive real numbers and 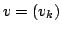 be any fixed sequence of non-zero complex numbers. If be any fixed sequence of non-zero complex numbers. If 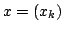 is any sequence of complex numbers we write is any sequence of complex numbers we write 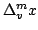 for the sequence of the for the sequence of the 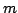 -th order differences of -th order differences of 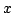 and and 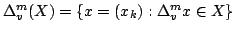 for any set for any set 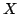 of sequences. In this paper we determine the of sequences. In this paper we determine the 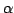 -, -, 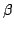 - and - and 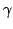 - duals of the sets - duals of the sets 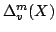 which are defined by Et et al. [2] for which are defined by Et et al. [2] for 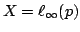 , , 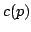 and and 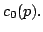 This study generalizes results of Malkowsky [9] in special cases. This study generalizes results of Malkowsky [9] in special cases.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|